Using Windows In FFT Analysis

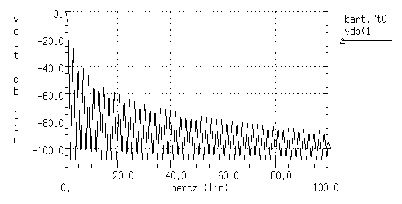
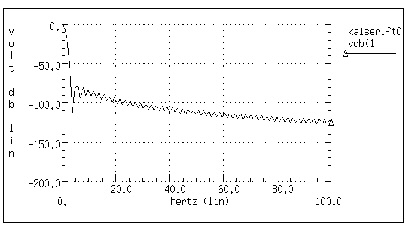
One problem with spectrum analysis in circuit simulators is that the duration of the signals is finite, although adjustable. Applying the FFT method to finite-duration sequences can produce inadequate results because of "spectral leakage," due primarily to the periodic extension assumption underlying DFT.

The effect occurs when the finite duration of the signal does not result in a sequence that contains a whole number of periods. This is especially true when FFT is used for signal detection or estimation - that is, for detecting weak signals in the presence of strong signals or resolving a cluster of equal strength frequencies.

In FFT analysis, "windows" are frequency weighting functions applied to the time domain data to reduce the spectral leakage associated with finite-duration time signals. Windows are smoothing functions that peak in the middle frequencies and decrease to zero at the edges, thus reducing the effects of the discontinuities as a result of finite duration. FFT Windows shows the windows available in Star-Hspice. Window Weighting Characteristics in FFT Analysis lists the common performance parameters for FFT windows available in Star-Hspice.

Figure 28-1: FFT Windows

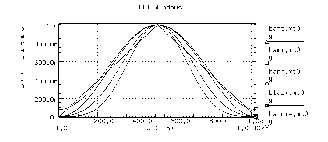
|NP is the number of points used for the FFT analysis.

The most important parameters in Window Weighting Characteristics in FFT Analysis are the highest side-lobe level (to reduce bias, the lower the better) and the worst-case processing loss (to increase detectability, the lower the better). Some compromise usually is necessary to find a suitable window filtering for each application. As a rule, the window performance improves with functions of higher complexity (those listed lower in the table). The Kaiser window has an ALFA parameter that allows adjustment of the compromise between different figures of merit for the window.

The simple rectangular window produces a simple bandpass truncation in the classical Gibbs phenomenon. The Bartlett or triangular window has good processing loss and good side-lobe roll-off, but lacks sufficient bias reduction. The Hanning, Hamming, Blackman, and Blackman-Harris windows use progressively more complicated cosine functions that provide smooth truncation and a wide range of side-lobe level and processing loss. The last two windows in the table are parameterized windows that allow you to adjust the side-lobe level, the 3 dB bandwidth, and the processing loss. For an excellent discussion of DFT windows, see Fredric J. Harris, "On the Use of Windows for Harmonic Analysis with Discrete Fourier Transform", Proceedings of the IEEE, Vol. 66, No. 1, Jan. 1978.

The characteristics of two typical windows are shown in Figures Bartlett Window Characteristics and Kaiser-Bessel Window Characteristics, ALFA=3.0.

Figure 28-2: Bartlett Window Characteristics

Figure 28-3: Kaiser-Bessel Window Characteristics, ALFA=3.0