Using Op-Amps, Comparators, and Oscillators

This section describes the benefits of using Star-Hspice's op-amps, comparators, and oscillators when performing simulation.

Star-Hspice Op-Amp Model Generator

Star-Hspice uses the model generator for the automatic design and simulation of both board level and IC op-amp designs. You can take the existing electrical specifications for a standard industrial operational amplifier, enter the specifications in the op-amp model statement, and Star-Hspice automatically generates the internal components of the op-amp to meet the specifications. You can then call the design from a library for a board level simulation.

The Star-Hspice op-amp model is a subcircuit that is about 20 times faster to simulate than an actual transistor level op-amp. You can adjust the AC gain and phase to within 20 percent of the actual measured values and set the transient slew rates accurately. This model does not contain high order frequency response poles and zeros and may significantly differ from actual amplifiers in predicting high frequency instabilities. Normal amplifier characteristics, including input offsets, small signal gain, and transient effects are represented in this model.

The op-amp subcircuit generator consists of two parts, a model and one or more elements. Each element is in the form of a subcircuit call. The model generates an output file of the op-amp equivalent circuit for collection in libraries. The file name is the name of the model (mname) with an .inc extension.

Once the output file is generated, other Star-Hspice input files may reference this subcircuit using a .SUBCKT call to the model name. The .SUBCKT call automatically searches the present directory for the file, then the directories specified in any .OPTION SEARCH ='directory_path_name', and finally the directory where the DDL (Discrete Device Library) is located.

The amplifier element references the amplifier model.

Convergence

If DC convergence problems are encountered with op-amp models created by the model generator, use the .IC or .NODESET statement to set the input nodes to the voltage halfway between the VCC and VEE. This balances the input nodes and stabilizes the model.

Op-Amp Element Statement Format

COMP=0 (internal compensation)

The syntax is:

xa1 in- in+ out vcc vee modelname AV=val

COMP=1 (external compensation)

The syntax is:

xa1 in- in+ out comp1 comp2 vcc vee modelname AV=val

in- the inverting input

in+ the noninverting input

out the output, single ended

vcc the positive supply

vee the negative supply

modelname the subcircuit reference name

Op-Amp .MODEL Statement Format

The syntax is:

.MODEL mname AMP parameter=value ...

mname model name. Elements reference the model by this name.

AMP identifies an amplifier model

parameter any model parameter described below

value value assigned to a parameter

Example

X0  IN-  IN+ OUT0  VCC VEE ALM124

 .MODEL ALM124 AMP

 +       C2=  30.00P     SRPOS=   .5MEG      SRNEG= .5MEG

 +       IB=  45N         IBOS=   3N           VOS=  4M

 +     FREQ=  1MEG      DELPHS=   25          CMRR=  85

 +     ROUT=  50            AV=   100K         ISC=  40M

 +    VOPOS=  14.5       VONEG=   -14.5        PWR=  142M

 +      VCC=  16           VEE=   -16         TEMP=  25.00

 +     PSRR=  100          DIS=   8.00E-16     JIS=  8.00E-16

Op-Amp Model Parameters

The model parameters for op-amps are shown below. The defaults for these parameters depend on the DEF parameter setting. Defaults for each of the three DEF settings are shown in the following table.

Names (Alias)	Units	Default	Description
AV (AVD)	volt/volt		Amplifier gain in volts out per volt in. It is the DC ratio of the voltage in to the voltage out. Typical gains are from 25k to 250k. If the frequency comes out too low, try increasing the negative and positive slew rates or decreasing DELPHS.
AV1K	volt/volt		Amplifier gain at 1 kilohertz. This is a convenient method of estimating the unity gain bandwidth. The gain can be expressed in actual voltage gain or in dB. Decibel is now a standard unit conversion for Star-Hspice. If AV1K is set, then FREQ is ignored. A typical value for AV1K is AV1K=(unity gain freq)/1000.
C2	farad		Internal feedback compensation capacitance. If the amplifier is internally compensated and no capacitance value is given, assume 30 pF. If the gain is high (above 500k), the internal compensation capacitor is probably different (typically 10 pF). If the amplifier is externally compensated, (COMP=1) set C2 to about 0.5 pF as the residual internal capacitance.
CMRR	volt/volt		Common mode rejection ratio. This is usually between 80 and 110 dB. This can be entered as 100 dB or as 100000.
COMP			Compensation level selector. This modifies the number of nodes in the equivalent to include external compensation nodes if set to one. See C2 for external compensation settings. COMP=0 internal compensation (Default) COMP=1 external compensation
DEF			Default model selector. Allows choice of three default settings. 0= generic (0.6 MHz bandwidth) (Default) 1= ua741 (1.2 MHz bandwidth) 2= mc4560 (3 MHz bandwidth)
DELPHS	deg		Excess phase at the unity gain frequency. Also called the phase margin . DELPHS is measured in degrees. Typical excess phases range from 5° to 50°. To determine DELPHS, subtract the phase at unity gain from 90°; this gives the phase margin. Use the same chart as used for the FREQ determination above. DELPHS interacts with FREQ (or AV1K). Values of DELPHS tend to lower the unity gain bandwidth, particularly values greater than 20°. The model does not have enough poles to always give correct phase and frequency response. It is usually best to pick the DELPHS closest to measured value that does not reduce unity gain bandwidth more than 20%.
DIS	amp	1e-16	Diode and BJT saturation current
FREQ (GBW, BW )	Hz		Unity gain frequency. Measured in hertz and typical frequencies range from 100 kHz to 3 MHz. If not specified, measure open loop frequency response at 0 dB voltage gain and the actual compensation capacitance. Typical compensation is 30 pF and single pole compensation configuration. If AV1K is greater than zero, the unity gain frequency is calculated from AV1K and FREQ is ignored.
IB	amp		Input bias current. The amount of current required to bias the input differential transistors. This is generally a fundamental electrical characteristic. Typical values are between 20 and 400 nA.
IBOS	amp		Input bias offset current, also called input offset current. This is the amount of unbalanced current between the input differential transistors. Generally a fundamental electrical characteristic. Typical values are 10% to 20% of the IB.
ISC	amp		Input short circuit current - not always specified. Typical values are between 5 and 25 mA. ISC can also be determined from output characteristics (current sinking) as the maximum output sink current. ISC and ROUT interact with each other, if ROUT is too large for a given value of ISC, ROUT is automatically reduced.
JIS	amp		JFET saturation current. Default=1e-16 and need not be changed.
LEVIN			Input level type selector. Allows only BJT differential pair creation. LEVIN=1 BJT differential input stage.
LEVOUT			Output level type selector. Allows only single-ended output stage creation. LEVOUT=1 single-ended output stage.
MANU			Manufacturer's name. This can be added to the model parameter list to identify the source of the model parameters. The name is printed in the final equivalent circuit.
PWR (PD)	watt		Total power dissipation value for the amplifier. This includes the calculated value for the op-amp input differential pair. If high slew rate and very low power is specified a warning is issued and the input differential pair alone gives the power dissipation.
RAC (r0ac, roac)	ohm		High frequency output resistance. This typically is about 60% of ROUT. RAC usually ranges between 40 to 70 ohms for op-amps with video drive capabilities.
ROUT	ohm		Low frequency output resistance. This can be determined using the closed loop output impedance graph. The impedance at about 1kHz, using the maximum gain, is close to ROUT. Gains of 1,000 and above show the effective DC impedance, generally in the frequency region between 1k and 10 kHz. Typical values for ROUT are 50 to 100 ohms.
SRNEG (SRN)	volt		Negative going output slew rate. This is found from the graph of the voltage follower pulse response. This is generally a 4 or 5 volt output change with 10 to 20 volt supplies. Measures the negative going change in voltage and the amount of time for the change.
SRPOS (SRP)	volt		Positive going output slew rate. This is found from the graph of the voltage follower pulse response. This is generally a 4 or 5 volt output change with 10 to 20 volt supplies. Measures the positive going change in voltage and the amount of time for the change. Typical slew rates are in the range of 70k to 700k.
TEMP	° C		Temperature in degrees Celsius. This usually is set to the temperature at which the model parameters were measured, which typically is 25 ° C .
VCC	volt		Positive power supply reference voltage for VOPOS. The amplifier VOPOS was measured with respect to VCC.
VEE	volt		Negative power supply voltage. The amplifier VONEG was measured with respect to VCC.
VONEG ( VON)	volt		Maximum negative output voltage. This is less than VEE (the negative power-supply voltage) by the internal voltage drop.
VOPOS (VOP)	volt		Maximum positive output voltage. This is less than VCC, the positive power supply voltage, by the internal voltage drop.
VOS	volt		Input offset voltage. This is the voltage required between the input differential transistors to zero the output voltage. This is generally a fundamental electrical characteristic. Typical values for bipolar amplifiers are in the range 0.1 mV to 10 mV. VOS is measured in volts. VOS can cause a failure to converge for some amplifiers. If this occurs, try setting VOS to 0 or use the initial conditions described above for convergence.

Op-Amp Model Parameter Defaults

Parameter	Description	Defaults
Parameter	Description	DEF=0	DEF=1	DEF=2
AV	Amplifier voltage gain	160k	417k	200k
AV1K	Amplifier voltage gain at 1 kHz	-	1.2 k	3 k
C2	Feedback capacitance	30 p	30 p	10 p
CMRR	Common mode rejection ratio	96 db 63.1k	106 db 199.5k	90 db 31.63k
COMP	Compensation level selector	0	0	0
DEF	Default level selector	0	1	2
DELPHS	Delta phase at unity gain	25°	17°	52°
DIS	Diode saturation current	8e-16	8e-16	8e-16
FREQ	Unity gain frequency	600 k	-	-
IB	Input bias current	30 n	250 n	40 n
IBOS	Input bias offset current	1.5 n	0.7 n	5 n
ISC	Output short circuit current	25 mA	25 mA	25 mA
LEVIN	Input circuit level selector	1	1	1
LEVOUT	Output circuit level selector	1	1	1
MANU	Manufacturer's name	-	-	-
PWR	Power dissipation	72 mW	60 mW	50 mW
RAC	AC output resistance	0	75	70
ROUT	DC output resistance	200	550	100
SRPOS	Positive output slew rate	450 k	1 meg	1 meg
SRNEG	Negative output slew rate	450 k	800 k	800 k
TEMP	Temperature of model	25 deg	25 deg	25 deg
VCC	Positive supply voltage for VOPOS	20	15	15
VEE	Negative supply voltage for VONEG	-20	-15	-15
VONEG	Maximum negative output	-14	-14	-14
VOPOS	Maximum positive output	14	14	14
VOS	Input offset voltage	0	0.3 m	0.5 m

Op-Amp Subcircuit Example

AUTOSTOP Option

This example uses the .OPTION AUTOSTOP option to shorten simulation time. Once Star-Hspice makes the measurements specified by the .MEASURE statement, the associated transient analysis and AC analysis stops whether or not the full sweep range for each has been covered.

AC Resistance

AC=10000G parameter in the Rfeed element statement installs a 10000 G feedback resistor for the AC analysis in place of the 10 k feedback resistor - used in the DC operating point and transient analysis - which is open-circuited for the AC measurements.

Simulation Results

The simulation results give the DC operating point analysis for an input voltage of 0 v and power supply voltages of ±15 v. The DC offset voltage is 3.3021 mv, which is less than that specified for the original vos specification in the op-amp .MODEL statement. The unity gain frequency is given as 907.885 kHz, which is within 10% of the 1 MHz specified in the .MODEL statement with the parameter FREQ. The required time rate for a 1 volt change in the output (from the .MEASURE statement) is 2.3 µs (from the SRPOS simulation result listing) providing a slew rate of 0.434 Mv/s. This compares to within about 12% of the 0.5 Mv/s given by the SRPOS parameter in the .MODEL statement. The negative slew rate is almost exactly 0.5 Mv/s, which is within 1% of the slew rate specified in the .MODEL statement.

Example

$$ FILE  ALM124.SP

.OPTION NOMOD AUTOSTOP  SEARCH=' '

.OP VOL

.AC DEC 10 1HZ  10MEGHZ

.MODEL PLOTDB   PLOT XSCAL=2 YSCAL=3

.MODEL PLOTLOGX PLOT XSCAL=2

.GRAPH AC MODEL=PLOTDB VM(OUT0)

.GRAPH AC MODEL=PLOTLOGX VP(OUT0)

.TRAN 1U 40US 5US .15MS

.GRAPH V(IN) V(OUT0)

.MEASURE TRAN 'SRPOS'     TRIG V(OUT0) VAL=2V RISE=1

+                         TARG V(OUT0) VAL=3V RISE=1

.MEASURE TRAN 'SRNEG'     TRIG V(OUT0) VAL=-2V FALL=1

+                         TARG V(OUT0) VAL=-3V FALL=1

.MEASURE AC   'UNITFREQ'  TRIG AT=1

+                         TARG VDB(OUT0) VAL=0 FALL=1

.MEASURE AC   'PHASEMARGIN'  FIND VP(OUT0)

+                         WHEN VDB(OUT0)=0

.MEASURE AC   'GAIN(DB)'      MAX VDB(OUT0)

.MEASURE AC   'GAIN(MAG)'     MAX VM(OUT0)

VCC   VCC GND  +15V

VEE   VEE GND  -15V

VIN IN  GND  AC=1 PWL 0US   0V 1US   0V 1.1US +10V 15US +10V

+  15.2US -10V 100US -10V

.MODEL ALM124 AMP

+       C2=  30.00P   SRPOS=     .5MEG       SRNEG=  .5MEG

+       IB=  45N       IBOS=   3N              VOS= 4M

+     FREQ=  1MEG    DELPHS=   25             CMRR= 85

+     ROUT=  50          AV=   100K            ISC=  40M

+    VOPOS=  14.5     VONEG=  -14.5            PWR= 142M

+      VCC=  16         VEE=  -16             TEMP= 25.00

+     PSRR=  100        DIS=    8.00E-16       JIS=  8.00E-16

Unity Gain Resistor Divider Mode

Rfeed  OUT0  IN- 10K AC=10000G

RIN     IN  IN- 10K

RIN+    IN+ GND 10K

X0  IN-  IN+ OUT0  VCC VEE ALM124

ROUT0  OUT0 GND    2K

COUT0  OUT0 GND  100P

.END

***** OPERATING POINT STATUS IS VOLTAGE   SIMULATION TIME IS     0.

  NODE     =VOLTAGE      NODE    =VOLTAGE      NODE  =VOLTAGE

+ 0:IN       =   0.      0:IN+  =-433.4007U 0:IN-  =  3.3021M

+ 0:OUT0     =   7.0678M 0:VCC  =  15.0000  0:VEE  = -15.0000

unitfreq    = 907.855K  TARG   = 907.856K  TRIG   =   1.000

PHASEMARGIN =  66.403

gain(db)    =  99.663   AT     =   1.000

FROM        =   1.000   TO     =  10.000X

gain(mag)   =  96.192K  AT     =   1.000

FROM        =   1.000   TO     =  10.000X

srpos       =   2.030U  TARG   =  35.471U  TRIG   =  33.442U

srneg       =   1.990U  TARG   =   7.064U  TRIG   =   5.074U

741 Op-Amp from Controlled Sources

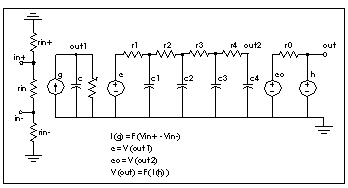
The µA741 op-amp is modeled by PWL controlled sources. The output is limited to ±15 volts by a piecewise linear CCVS (source "h").

Figure 26-24: Op-Amp Circuit

Example

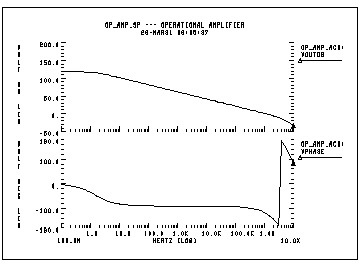
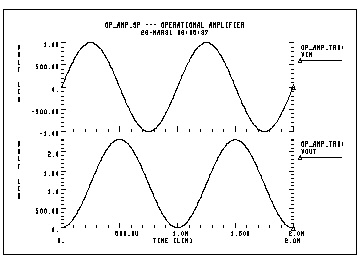
0p_amp.sp --- operational amplifier

.options post=2

.tran .001ms 2ms

.ac dec 10 .1hz 10me'

*.graph tran vout=v(output)

*.graph tran vin=v(input)

*.graph ac model=grap voutdb=vdb(output)

*.graph ac model=grap vphase=vp(output)

.probe tran vout=v(output) vin=v(input)

.probe ac voutdb=vdb(output) vphase=vp(output)

.model grap plot xscal=2

Main Circuit

xamp input 0 output opamp

vin input 0 sin(0,1m,1k) ac 1

* subcircuit definitions

* input subckt

.subckt opin in+ in- out

rin  in+ in- 2meg

rin+ in+ 0 500meg

rin- in- 0 500meg

g 0 out pwl(1) in+ in- -68mv,-68ma 68mv,68ma delta=1mv

c out 0 .136uf

r out 0 835k

.ends

RC Circuit With Pole At 9 MHz

.subckt oprc in out

e out1 0 in 0 1

r1 out1 out2 168

r2 out2 out3 1.68k

r3 out3 out4 16.8k

r4 out4 out 168k

c1 out2 0 100p

c2 out3 0 10p

c3 out4 0 1p

c4 out 0 .1p

r out 0 1e12

.ends

Output Limiter to 15 v

.subckt opout in out

eo out1 0 in 0 1

ro out1 out 75

vdum out dum 0

h dum 0 pwl(1) vdum delta=.01ma -.1ma,-15v .1ma,15v

.ends

* op-amp subckt

.subckt opamp in+ in- out

xin in+ in- out1 opin

xrc out1 out2 oprc

xout out2 out opout

.ends

.end

Figure 26-25: AC Analysis Response

Figure 26-26: Transient Analysis Response Chua & Lin. Computer Aided Analysis of Electronic Circuits. Englewood Cliffs: Prentice-Hall, 1975, page 117. See also "SPICE2 Application Notes for Dependent Sources," by Bert Epler, IEEE Circuits & Devices Magazine, September 1987.

Inverting Comparator with Hysteresis

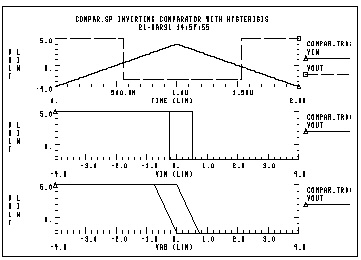
An inverting comparator is modelled by a piecewise linear VCVS.

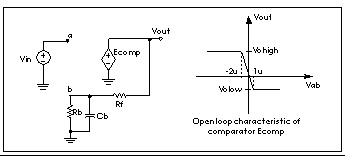
Figure 26-27: Inverting Comparator with Hysteresis

Two reference voltages corresponding to volow and vohigh of Ecomp characteristic are:

When Vin exceeds Vrefhigh, the output Vout goes to Volow. For Vin less than Vreflow, the output goes to Vohigh.

Example

Compar.sp Inverting comparator with hysterisis

.OPTIONS POST PROBE

.PARAM  vohigh=5v volow=-2.5v rbval=1k rfval=9k

Ecomp  out 0 PWL(1) a  b   -2u,vohigh  1u,volow

Rb  b  0   rbval

Rf  b  out rfval

Cb  b  0 1ff

Vin a  0 PWL(0,-4 1u,4 2u,-4)

.TRAN .1n  2u

.PROBE Vin=V(a) Vab=V(a,b) Vout=V(out)

.END

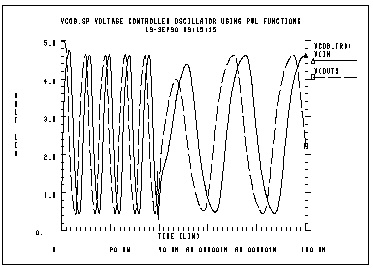
Figure 26-28: Response of Comparator

Voltage Controlled Oscillator (VCO)

In this example, a one-input NAND functioning as an inverter models a five stage ring oscillator. PWL capacitance is used to switch the load capacitance of this inverter from 1pF to 3 pF. As the simulation results indicate, the oscillation frequency decreases as the load capacitance increases.

Example

vcob.sp voltage controlled oscillator using pwl functions

.OPTION POST

.GLOBAL ctrl

.TRAN 1n 100n

.IC V(in)=0 V(out1)=5

.PROBE TRAN V(in) V(out1) V(out2) V(out3) V(out4)

X1 in out1 inv

X2 out1 out2 inv

X3 out2 out3 inv

X4 out3 out4 inv

X5 out4 in inv

Vctrl ctrl 0 PWL(0,0 35n,0 40n,5)

Subcircuit Definition

.SUBCKT inv in out rout=1k

* The following G Element is functioning as PWL capacitance.

Gcout out 0 VCCAP PWL(1) ctrl 0  DELTA=.01

+ 4.5 1p

+ 4.6 3p

Rout out 0 rout

Gn 0 out NAND(1) in 0 SCALE='1.0k/rout'

+ 0. 5.00ma

+ 0.25 4.95ma

+ 0.5 4.85ma

+ 1.0 4.75ma

+ 1.5 4.42ma

+ 3.5 1.00ma

+ 4.000 0.50ma

+ 4.5 0.20ma

+ 5.0 0.05ma

.ENDS inv

.END

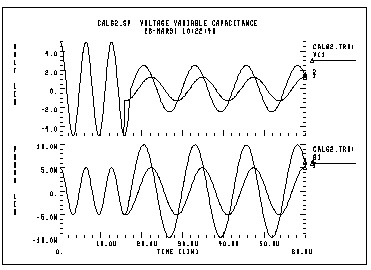
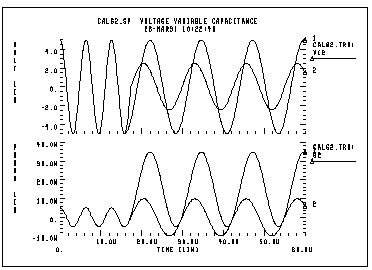
Figure 26-29: Voltage Controlled Oscillator Response

LC Oscillator

The capacitor is initially charged to 5 volts. The value of capacitance is the function of voltage at node 10. The value of capacitance becomes four times higher at time t2. The frequency of this LC circuit is given by:

At time t2, the frequency must be halved. The amplitude of oscillation depends on the condition of the circuit when the capacitance value changes. The stored energy is:

Assuming at time t2, when V=0, C changes to A · C, then:

and from the above equation:

The second condition to consider is when V=Vin, C changes to A· C. In this case:

Therefore, the voltage amplitude is modified between Vm/sqrt(A) and Vm/A depending on the circuit condition at the switching time. This example tests the CTYPE 0 and 1 results. The result for CTYPE=1 must be correct because capacitance is a function of voltage at node 10, not a function of the voltage across the capacitor itself.

Example

calg2.sp voltage variable capacitance

.OPTION POST

.IC v(1)=5 v(2)=5

C1 1 0 C='1e-9*V(10)' CTYPE=1

L1 1 0 1m

C2 2 0 C='1e-9*V(10)' CTYPE=0

L2 2 0 1m

V10 10 0 PWL(0sec,1v t1,1v t2,4v)

R10 10 0 1

.TRAN .1u 60u UIC SWEEP DATA=par

.MEAS TRAN period1 TRIG V(1) VAL=0 RISE=1

+ TARG V(1) VAL=0 RISE=2

.MEAS TRAN period2 TRIG V(1) VAL=0 RISE=5

+ TARG V(1) VAL=0 RISE=6

.PROBE TRAN V(1) q1=LX0(C1)

.PROBE TRAN V(2) q2=LX0(C2)

.DATA par t1 t2

15.65us 15.80us

17.30us 17.45us

.ENDDATA

.END

Figure 26-30: Correct Result Corresponding to CTYPE=1

Figure 26-31: Incorrect Result Corresponding to CTYPE=0

Star-Hspice Manual - Release 2001.2 - June 2001