Using Analog Behavioral Elements

The following components are examples of analog behavioral building blocks. Each demonstrates a basic Star-Hspice feature:

Behavioral Integrator

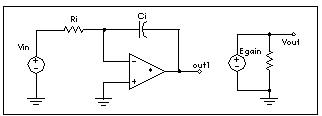
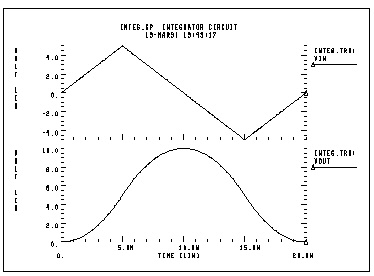
The integrator circuit is modelled by an ideal op-amp and uses a VCVS to adjust the output voltage. The output of integrator is given by:

Figure 26-14: Integrator Circuit

Example

Integ.sp  integrator circuit

Control and Options

.TRAN 1n 20n

.OPTIONS  POST PROBE  DELMAX =.1n

.PROBE Vin=V(in) Vout=V(out)

Subcircuit Definition

.SUBCKT integ  in out  gain=-1 rval=1k cval=1p

EOP  out1  0  OPAMP   in-  0 

Ri in  in-  rval

Ci in- out1 cval 

Egain out 0 out1 0 gain

Rout  out 0 1e12

.ENDS

Circuit

Xint in out  integ  gain=-0.4

Vin in  0  PWL(0,0 5n,5v 15n,-5v 20n,0)

.END

Figure 26-15: Response of Integrator to a Triangle Waveform

Behavioral Differentiator

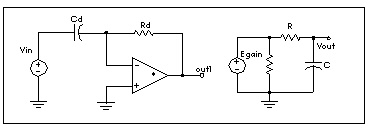
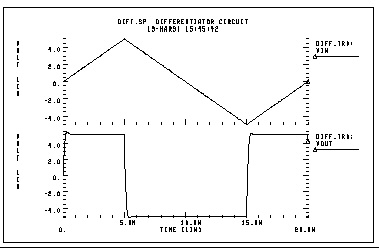
A differentiator is modelled by an ideal op-amp and a VCVS for adjusting the magnitude and polarity of the output. The differentiator response is given by:

For a high-frequency signal, the output of a differentiator can have overshoot at the edges. You can smooth this out using a simple RC filter.

Figure 26-16: Differentiator Circuit

Example

Diff.sp  differentiator circuit

* V(out)=Rval * Cval * gain * (dV(in)/dt)

Control and Options

.TRAN 1n 20n

.PROBE  Vin=V(in)  Vout=V(out)

.OPTIONS PROBE POST 

Differentiator Subcircuit Definition

.SUBCKT diff in out  gain=-1 rval=1k cval=1pf

EOP  out1  0  OPAMP   in-  0 

Cd in  in-  cval

Rd in- out1 rval 

Egain out2 0 out1 0 gain

Rout  out2 0 1e12

*rc filter to smooth the output

R out2 out 75

C out  0   1pf

.ENDS

Circuit

Xdiff in out  diff  rval=5k 

Vin in  0  PWL(0,0 5n,5v 15n,-5v 20n,0)

.END

Figure 26-17: Response Of a Differentiator to a Triangle Waveform

Ideal Transformer

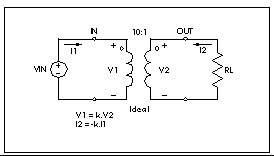
The following example uses the ideal transformer to convert 8 ohms impedance of a loudspeaker to 800 ohms impedance, which is a proper load value for a power amplifier, Rin=n 2 · RL.

MATCHING IMPEDANCE BY USING IDEAL TRANSFORMER

E  OUT 0 TRANSFORMER  IN 0   10 

RL OUT 0 8

VIN IN 0 1

.OP

.END

Figure 26-18: Ideal Transformer Example

Behavioral Tunnel Diode

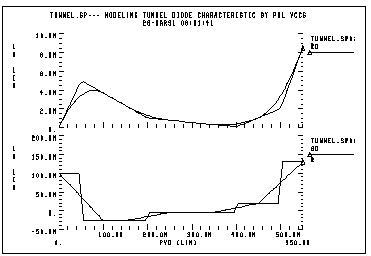
In the following example, a tunnel diode is modeled by a PWL VCCS. The current characteristics are obtained for two DELTA values (50 µv and 10 µv). The IV characteristics corresponding to DELTA=10 µv have sharper corners. The derivative of current with respect to voltage (GD) is also displayed. The GD value around breakpoints changes in a linear fashion.

Example

tunnel.sp-- modeling tunnel diode characteristic by pwl vccs

* pwl function is tested for two different delta values. The 

* smaller delta will create the sharper corners.

.options post=2

vin 1 0 pvd

.dc pvd 0 550m 5m sweep delta poi 2 50mv 5mv

.probe dc id=lx0(g) gd=lx2(g)

g 1 0 pwl(1) 1 0 delta=delta

+ -50mv,-5ma 50mv,5ma 200mv,1ma 400mv,.05ma

+ 500mv,2ma 600mv,15ma 

.end

Figure 26-19: Tunnel Diode Characteristic

Behavioral Silicon Controlled Rectifier (SCR)

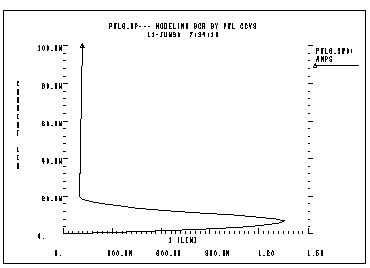
The silicon controlled rectifier (SCR) characteristic can be easily modeled using a PWL CCVS because there is a unique voltage value for any current value.

Example

pwl6.sp--- modeling SCR by pwl ccvs

*The silicon controlled rectifier (SCR) characteristic

*is modelled by a piecewise linear current controlled

*voltage source (PWL_CCVS), because for any current value

*there is a unique voltage value.

*

*use iscr as y-axis and v(1) as x-axis

*

.options post=2

iscr 0 2 0

vdum 2 1 0 

.dc iscr 0 1u 1n

.probe vscr=lx0(h) transr=lx3(h)

h 1 0 pwl(1) vdum -5na,-2v 5na,2v 15na,.1v 1ua,.3v 10ua,.5

+ delta=5na

.end

Figure 26-20: Silicon Controlled Rectifier

Behavioral Triode Vacuum Tube Subcircuit

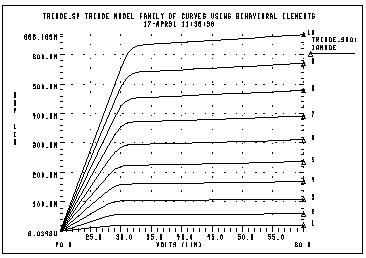
The following example shows how to include the behavioral elements in a subcircuit to give very good triode tube action. The basic power law equation (current source gt) is modified by the voltage source ea to give better response in saturation.

Example

triode.sp triode model family of curves using behavioral elements

Control and Options

.options post acct 

.dc va 20v 60v 1v vg 1v 10v 1v

.probe ianode=i(xt.ra) v(anode) v(grid) eqn=lv6(xt.gt)

.print v(xt.int_anode) v(xt.i_anode) inode=i(xt.ra) eqn=lv6(xt.gt) 

Circuit

vg grid 0 1v

va anode 0 20v

vc cathode 0 0v

xt anode grid cathode triode

Subcircuit Definition

.subckt triode anode grid cathode

* 5 ohm anode resistance

* ea creates saturation region conductance

ra anode i_anode 5

ea int_anode cathode pwl(1) i_anode cathode delta=.01

+ 20,0 27,.85 28,.95 29,.99 30,1 130,1.2 

gt i_anode cathode 

+ cur='20m*v(int_anode,cathode)*pwr(max(v(grid,cathode),0),1.5)' 

cga grid i_anode 30p

cgc grid cathode 20p

cac i_anode cathode 5p

.ends

*

.end

Figure 26-21: Triode Family of Curves

Behavioral Amplitude Modulator

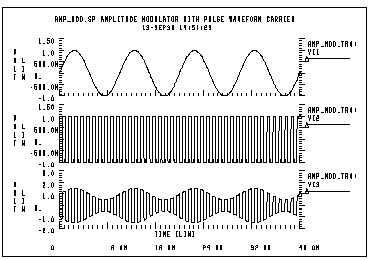
This example uses a G Element as an amplitude modulator with pulse waveform carrier.

Example

amp_mod.sp amplitude modulator with pulse waveform carrier

.OPTIONS POST

.TRAN .05m 40m

.PROBE V(1) V(2) V(3)

Vs 1 0 SIN(0,1,100)

Vc 2 0 PULSE(1,-1,0,1n,1n,.5m,1m)

Rs 1 0 1+

Rc 2 0 1

G 0 3 CUR='(1+.5*V(1))*V(2)'

Re 3 0 1

.END 

Figure 26-22: Amplitude Modulator Waveforms

Behavioral Data Sampler

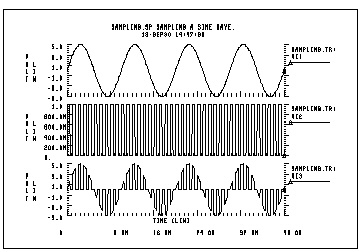
A behavioral data sample follows.

Example

sampling.sp sampling a sine wave.

.OPTIONS POST

.TRAN .05m 40m

.PROBE V(1) V(2) V(3)

Vc 1 0 SIN(0,5,100)

Vs 2 0 PULSE(0,1,0,1n,1n,.5m,1m)

Rc 1 0 1

Rs 2 0 1

E 3 0 VOL='V(1)*V(2)'

Re 3 0 1

.END

Figure 26-23: Sampled Data